|
The following was presented to many engineering symposia and meetings and nearly no medical ones (except in clipped and heavily washed form). A portion of it did get published (Contralateral Compensation with Knee Impairment - Clinical Orthopedics & Related Research, October 1987)
This was an especially difficult study to perform, to sort out, and close to impossible to publish. Only a small bit of it was reported in journal form. Over 300 two foot wide pages of dense spreadsheet crunched data
were generated by a series of experiments aimed at revealing how compensatory mechanisms dealt with limited range of motion.
Of greatest interest was whether Inman's so called "determinants of gait" would hold up. If not, where did they fail? The main focus of Inman's determinants were leg mechanisms that reduced the vertical rise of the
up-down-up bobble of human walking and which smoothed them into a sine wave path. A low amplitude sine wave travel of the center of mass at uniform travel was a least energy path.
In these experiments Drs Noshir Langrana, Jack Jolly From Rutgers engineering and myself first went after single sided impairments of range of motion of the knee. What did that look like? Would the impaired side use
as much of the range as it could and the rest just fall on the usual path? That is, was it the apple after the bite? The other unimpaired leg would do what? It was the "normal" side. So would it act "normal"
or would we see the normal side do something else? Would the apple pop like a balloon?

The first series studied two case types. Sequential loss of flexion range and sequential loss of extension range.
Some findings were startling. In very thin kids with minimally padded casts from groin to ankle glued with surgical adhesive directly to skin (with knee marker made visible) at least 15 degrees of knee
flexion was always possible. Put another way, without flaying the subjects, their muscle thickness made full knee immobilization by even an extreme brace nearly impossible. Actual ranges exceeded the
braced limitations.
In the course of a single day, metal failure happened many times requiring swapping in new metal parts to the devices indicating that stresses and strains were very high.
 Right off the bat, a conclusion was looming.
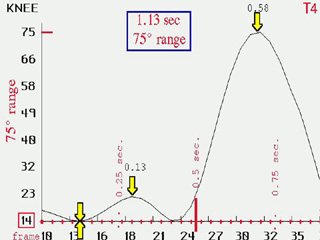
From another study we see (left) knee range under slight tension. Even so, the range needed for stance phase is minimal (between 14 to 23 degrees, a total of 9 degrees). Right off the bat, a conclusion was looming.
From another study we see (left) knee range under slight tension. Even so, the range needed for stance phase is minimal (between 14 to 23 degrees, a total of 9 degrees).
Without such tension the baseline would show stance to go from zero to maybe 15 degrees. So we can say that stance phase knee flexion is hard to impede (even with our cast from hell).
Inman's determinants, interestingly, were mostly dealing with stance phase mechanics. It is hard to thwart them.
 However, the big bump is the 70 to 80 degrees of knee
flexion required during swing phase. Swing phase is range-wise robust and easily reigned in. However, the big bump is the 70 to 80 degrees of knee
flexion required during swing phase. Swing phase is range-wise robust and easily reigned in.
Knee flexion hugs the normal range curve (each youngster used their own normal curve) and strives to maintain phase (timing with the other leg which is in stance while the fettered
leg is in swing). Well, you can't swing two legs at different rates. One can't be taking 1 1/2 steps to the other's 1 step.
The free leg would mirror the fettered leg to promote symmetry. By the way, there is this big MYSTERY as to why we biologically prefer mates who show symmetry. Duh. We need it! More
about this later. The issues that evolve in the well leg, so to speak, are those that bring symmetry to periodicity with allowance for the imposed oddities of clearance.
The other very unexpected finding was observed because we didn't
"normalize" time in all of our graphs. The data was graphed twice. Once with time as time and again with the x-axis divided up in percentage with 100% being one full stride cycle. This commonly used
second form hides subtle phase shift mechanisms. We logged all events on these true time graphs, where events were not just heel and toe strike, heel and toe rise, 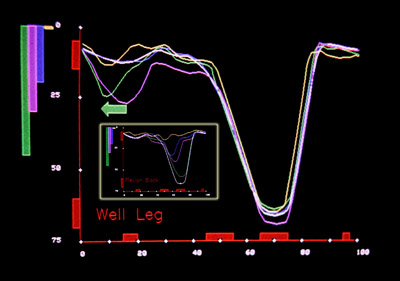 but also interrelationships such as
verticality of the line between hip and ankle or center of mass and floor support center. What a small bump in the flexion curve did depended on where it was centered on vertical relationships (hip above ankle). but also interrelationships such as
verticality of the line between hip and ankle or center of mass and floor support center. What a small bump in the flexion curve did depended on where it was centered on vertical relationships (hip above ankle).
Shifting the same degree of flexion left or right, same bump height in the graph, produced more or less vertical clearance depending on the way the shift went. This was true of either leg. A leg impaired
by way of range limitation can still, given intact neural mechanisms, alter timing to enhance or decrease rise. Inman's criteria were the
NORMAL determinants, of mostly stance and mumble mumble swing on level surfaces in no wind with nobody pestering you. Ideal. Ideal and aimed mostly at getting a stable prosthesis for amputees.
By the way, in the elastic studies, there are no impediments on the ankles at all. Yet, we saw early toe
walking as a compensatory mechanism. This phase shift phenomenon was already understood by us from these studies but we had to rethink of it as a mechanism in dampened or resisted movement as
opposed to blocked range.
 Another totally confusing finding
was that often the "circumducting" leg is adducting. We were so sure this was an error that the programming got rewritten three times by me to make the error go away. Another totally confusing finding
was that often the "circumducting" leg is adducting. We were so sure this was an error that the programming got rewritten three times by me to make the error go away.
It persisted. The strobe rendering of what was happening immediately gave it away (after a wasted month) whereas the numbers were not to be believed.
The swinging leg has mass and inertia. The 'circumduction' was more likely to arise from the raising of the pelvis on the braced leg side by action of the free hip on the far side away from the circumducting
leg along with a lateral shift. The swinging leg doing nothing but continuing on in its swing shows relative
adduction by way of its hip raising (and pelvis tilting). Sometimes it would swing out, but more often it just was carried higher by a side shift to the other side by the other leg's action.
From this was the first clue of just how much apparent hip and leg motion can appear to come from the involved side when in reality it may all be coming from the opposite side by way of stiff linkage. In a
dense (very stiff) right hemiplegia, the entire right side moves as a single unit around the left hip. What
looks like right hip flexion is backward lean from the left stance leg through the left hip.
However, neither movement patterns nor EMG in this series looked like any CP we have seen. Range of motion deficits are joint stressful but far less disabling than motion damping or loss of control.
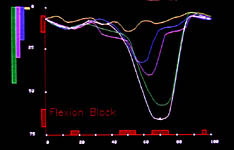
Here are some of the results from the single knee flexion block and extension block runs. There were 4 subjects, two boys and two girls.
The bar graphs on the left indicate the device range that is allowed by the device for that trial color coded to the data plotted on the right.
The smaller inset box shows the leg with the confining brace while the larger graph is of the free (unfettered) leg. Notice that both legs seek out the "normal" swing phase curve to the extent allowed
by constraint. The braced leg is forced into more flexion seen well in stance phase. The free leg mirrors that somewhat and uses a skew pelvis shift to normalize the rest (a skew will produce apparent
shortening and equalize the two legs further as to height). Swing phase timing appears to be important.
The reverse constraints, those of blocking flexion but allowing knee extension are shown next.
Again the free leg (well leg or normal leg) is shown large with the fettered leg shown in the inset. Successive loss of range causes the blocked leg to hug the flexion curve with little effect on stance.
Flexion blocks disturb the involved leg swing substantially and we see the well leg playing tricks to clear the swinging other side. A leftward (earlier) knee stance flexion extension is seen with
exaggerated height. A key finding is the small wobble that becomes more obvious at the juncture of the small stance bump and the tall swing valley. See the next image:
This curious wobble in the knee flexion graph comes from the foot. This is the data telling us that the knee range of motion is NOT a product of knee extensors and knee flexors but a complex soup
including passive effects from afar (including foot reaction on the floor below, in this case phase shift includes toe walking) and from the hip above.
 What was very worrysome to us was that
published data from many other labs lacked this wobble. I then looked to the math. Gait labs are products and products want to look good. Bumpy lines look, well, bumpy. Many commercial devices
don't show the raw data but rather a spline fit of that data. Was the spline killing the curious wobble? What was very worrysome to us was that
published data from many other labs lacked this wobble. I then looked to the math. Gait labs are products and products want to look good. Bumpy lines look, well, bumpy. Many commercial devices
don't show the raw data but rather a spline fit of that data. Was the spline killing the curious wobble?
A study of data plotting methods with attention to curve characteristics was then undertaken. Actual data was made smooth to the eye and used as a data model. This was the 'data known by God'.
Copies were made with many degrees and kinds of noise and sampling rate variations added to make the data - dirty, that is more real. Then the methods available to clean that data were used to see if the
cleaned up curve would match the divine original.
 The divine line on the left is dense
white. Squiggly noise added to it can be like the fuzz on a peach or like quills on a porcupine. The divine line on the left is dense
white. Squiggly noise added to it can be like the fuzz on a peach or like quills on a porcupine.
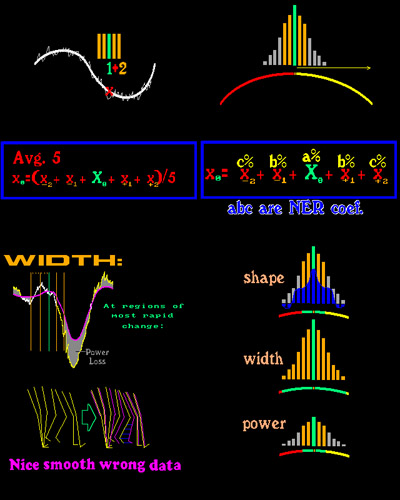
Averaging methods look at a span of data and total them then divide by the span (look at five points, add them, divide by 5) put that value as the central value (3rd) in a copy of the data.
But below we see the "power loss" that happens if the span of averaging is wider than the event you wish to see. Data from both sides knocks down or fills in the event which goes away. This is a
number version of a capacitor.
If instead, you look at a span and give greater weight to neighboring values than to the far away ones a better fit occurs. But what proportional weight? Bessel functions can be used >> IF <<
they are matched well to what you KNOW is going on. But how do you know?
By not being in a hurry. Computers are fast and can look three or whatever times through the data to
get a sense of reversals, width of those changes and the maintenance of the power of the original curve.
I ran a Bessel first pass Nearly Equal Ripple (NER) evaluation which sets up my own moving Tangent (first derivative) which alters the smoothing bell as it traverses the data and which makes certain that
baselines stay put and power is exactly maintained.
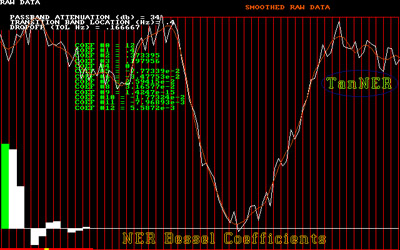 Here a porcupine (very noisy and
low sampling rate) data set is used to generate the improved curve. It is nearly identical to the divine original. Here a porcupine (very noisy and
low sampling rate) data set is used to generate the improved curve. It is nearly identical to the divine original.
Lower left we see the 'bell' values used by the TanNER function to shape the data
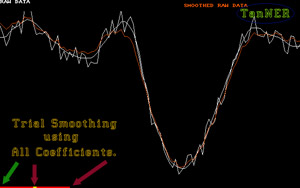 A simple graphic red line (lower left edge) indicates
the span of the moving TanNer function and the yellow spot in the center the relative weight of its effect and lateral scope. A simple graphic red line (lower left edge) indicates
the span of the moving TanNer function and the yellow spot in the center the relative weight of its effect and lateral scope.
Now, don't you fell better? You do. Comon, you enjoyed this. Right?
So now the small red boxes that sit along the graph bases are exposed. They are the found event ranges that require the most care and they correspond very well to >> EVENTS <<. That is, passive
things that happen from afar which show up in curves that don't seem to be related at first thought.
You getting this? I can change the way my KNEE moves by doing something with my foot! So too with my hip. We are beginning to capture COMPENSATORY events - these are the fowl in the bush which we are hunting.
How do they work? This gets deep folks and gets into Copernicus, Phidias (built the Parthenon) and Fibonacci along with the golden proportion, symmetry, and lust.
Lust? I think so.
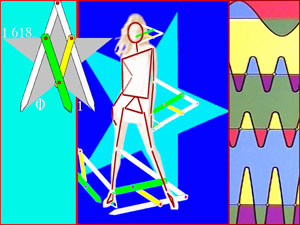
Phidias is often credited with making the golden proportion popular. The Parthenon uses it in the major rectangles. You can kind of pick your targets and make it more or less true, but the big obvious
weighted centers fall very close upon a golden rectangle (sides in ratio of 1 to 1.618).
That number is called Phi after Phidias who didn't know that number. They didn't have decimal math.
Geez. It was a geometric thing. If you take a line and divide it at just the right place, the the larger hunk
is in proportion to the smaller hunk as the entire (large +small) is to the larger hunk. You can keep
using that ratio and dividing remainders smaller and smaller and it looks like what? Everything in nature. Ferns, pine cones whatever.
So Phidias did that?
No.
 How do we know? He told us. He said he took
the proportions - ready for this - of the Parthenon from "women pleasing to my eye". How do we know? He told us. He said he took
the proportions - ready for this - of the Parthenon from "women pleasing to my eye".
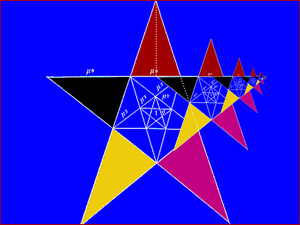
It is easy to construct a calliper in this proportion using a five pointed star (the star of - who else - Venus) as the five pointed star runs amoc with 1.618 relationships. Yeah, but was this actually used
? Yes. Using a shovel you can dig them up. There's no mystery here. They were used by architects, artists, sculptors and who knows who else.
Psychologists had run many preference tests on simple shapes and 1.618 always wins. We like it. We
like people who look like it. We make ourselves, over time, look like it by liking it. So what does it do?
 It is a very highly reentrant number. That is, using a
very simple rule of dividing up a single thing - or process - we get a remainder which can do it again without unmatched left overs. It is a very highly reentrant number. That is, using a
very simple rule of dividing up a single thing - or process - we get a remainder which can do it again without unmatched left overs.
It is crazy efficient for stacking. Also if you want to be able to fit two curves simultaneously (the intended path of travel and the shape of the unsmoothened earth surface) using the fewest rules
and few parts then how about a cascade of one rule using parts in proportion to 1.618? THAT is what we are. We have the math in our heads to
spin off what is needed - on the fly - to traverse the earth with all its rugged features and do so efficiently. It is the efficiency that make us so extraordinary.
A mathematical model which uses a series of parts in Fibonacci series will match walking data from normals AND abnormals. Remember, when the folks with impairments are walking they ARE
WALKING. Even broken, we 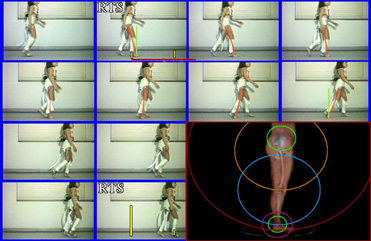 out perform all the beasts on this planet at this upright task - because
we have the math in our heads and the limbs in optimum proportion to exploit it. out perform all the beasts on this planet at this upright task - because
we have the math in our heads and the limbs in optimum proportion to exploit it.
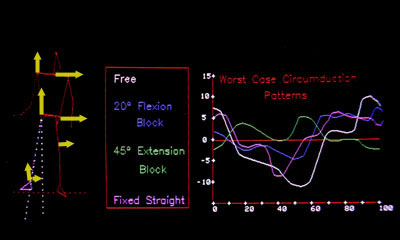
Plotted in polar graph style the "harmonics" (component circular portions) simply jump out.
In this form we can see which spokes (femur, tibia etc) of our wheels are generating what effects and whether they are being used in pairs to generate larger harmonics to solve the
problem at hand - getting there.
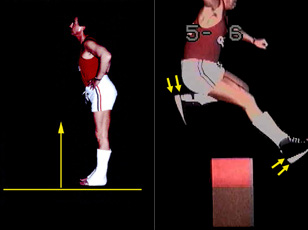 In a rather extreme study of restricted arc, we used very snug casts set in 'equinus' (pointing the forefoot downward). Our subjects could not
really walk at all, but did stumbling falling lunges. Fatigue was immediate and severe. In a rather extreme study of restricted arc, we used very snug casts set in 'equinus' (pointing the forefoot downward). Our subjects could not
really walk at all, but did stumbling falling lunges. Fatigue was immediate and severe.
Stance was very typical for all the subjects, male and female. We called it jack-knife. They flex at the hips so as to not fall over backward. This posture, by the way, is often attributed to weak
trunk in kids with motor problems. Far more often than not, the hip flexion excess is just a manifestation of the ankle equinus posture.
We then tried a variety of specially shaped and equipped shoes. Essentially the data which was found to be true for prosthetics was found to be true for solid ankle anything, including casts. Get, those
mechanics right, by a compensating shoe angle with heel cushion and normal function returns. In this case a control arc is equal to zero but simply centered in phase with what is above.
|